Create recursion-schemes using comonads
In today's post, I explain how comonads can be used to create a tailor-made recursion scheme to perform computations based on multiple simultaneous folds over a single recursive data type.
The technique is based on the theoretical heavy paper named "Recursion Schemes from Comonads", but I will try to explain it as much as possible in an approachable way from a pragmatic point of view. I will assume some familiarity with Haskell and the recursion-schemes library though, to avoid this article from exploding in size. If you are interested and want to learn more about the nitty-gritty details of the recursion-schemes library explained in an accessible way, I can recommend Patrick Thomson's great 6-part series of recursion-scheme blogposts.
The case for generalized recursion schemes
Before I explain the technique, I have to point out that most usecases can probably be covered by an already existing recursion scheme provided by the recursion-schemes library. Always try to use an existing scheme where possible, since it is just much simpler and easier to maintain over time!
However, recently when I was working on my Datalog compiler, I ran into some situations where functions like zygo and para would not be powerful enough. I'd notice this when I had to do a lot of additional "bookkeeping" and maintain a lot of extra state in the fold itself. If you notice yourself that you are running into a similar situation when writing code that uses recursion-schemes, that might be a signal you need to upgrade to a custom-built scheme.
Creating a custom recursion scheme
If we search through the recursion-schemes library, we come across a gcata function (short for generalized catamorphism or fold) with a gnarly type signature:
gcata :: (Recursive t, Comonad w)
-- A "distributive law":
=> (forall b. Base t (w b) -> w (Base t b))
-- A (Base t)-w-algebra:
-> (Base t (w a) -> a)
-- A structure to recurse over and collect results:
-> t
-- The result:
-> aThe signature tells us the following: if we pass in a "distributive law" that describes what actions to perform at each node of a recursive datastructure, and if we pass in an algebra for transforming a single layer of a recursive structure to a value, then we can fold down the entire recursive structure down to a single result value.
The recursion-schemes library provides us with many distributive laws and even distributive law transformers for composing these distributive laws (e.g. distZygoT, distPara). If you pass in one of these values to gcata, the resulting behavior of the function will adapt itself:
-- distZygoT + distPara gives us a recursion scheme:
-- 1. f is a helper algebra for computing a value "b"
-- 2. g is a algebra that gives access to "b", the original structure "t"
-- and can be used to compute an "a"
example
:: (Recursive t, Corecursive t)
=> (Base t b -> b)
-> (Base t (EnvT b ((,) t) a) -> a)
-> t
-> a
example f g = gcata (distZygoT f distPara) gThese distributive law combinators get us really far. But for my usecase, this still wasn't enough. I needed to write a compiler pass, where I needed to do 2 helper folds and 1 final fold that had access to the results of the previous 2 folds. On top of that, both the final fold and one of the helper folds needed access to the original recursive structure for some computations. So let's see how we can create a recursion scheme to do just that.
Since the distributive law argument passed to gcata can make use of any Comonad, we can introduce our own datastructure to create exactly the behavior we need. In the situation I just mentioned, the datastructure needs access to four distinct values:
- The original recursive datastructure,
- The result from the first helper fold,
- The result from the second helper fold,
- The result from the final fold.
Let's create a datastructure that helps us do just that:
-- NOTE: Quad is isomorphic to a tuple with 4 elements (a, b, c, d).
-- We need a custom data type though, since the tuple type does not implement
-- Comonad.
data Quad a b c d
= Quad
{ qFirst :: a
, qSecond :: b
, qThird :: c
, qFourth :: d
} deriving Functor
instance Comonad (Quad a b c) where
extract (Quad _ _ _ d) = d
duplicate (Quad a b c d) =
Quad a b c (Quad a b c d)Next up, we need to write our own distributive law that makes use of the Quad data type. First of, here's the type signature, annotated with some comments:
distributiveLaw
:: Corecursive t
-- Given a first helper (Base t)-algebra:
=> (Base t a -> a)
-- and a second helper (Base t)-algebra, which also has access to
-- the original subtree "t":
-> (Base t (t, b) -> b)
-- then we get a distributive law that manages all the subresults
-- using the Quad data type:
-> (Base t (Quad t a b c) -> Quad t a b (Base t c))While this type signature is definitely complicated, it's actually quite straight-forward and mechanical to implement in a correct way using hole driven development. This is due to the fact that the types are so general and we only have a handful of functions (from the Corecursive and Functor type classes that we can use to transform the data.
distributiveLaw
:: Corecursive t
=> (Base t a -> a)
-> (Base t (t, b) -> b)
-> (Base t (Quad t a b c) -> Quad t a b (Base t c))
distributiveLaw f g base_t_quad =
-- 1. we fmap an accessor function to only look at parts of `Quad`:
let base_t_t = fmap qFirst base_t_quad
base_t_a = fmap qSecond base_t_quad
-- 2. `(&&&)` + `qFirst` gives easy access to the original structure:
base_t_tb = fmap (qFirst &&& qThird) base_t_quad
base_t_c = fmap qFourth base_t_quad
-- 3. `embed` is used to get back the original recursive structure
-- 4. apply the helper algebras `f` and `g` to collect our sub-results
in Quad (embed base_t_t) (f base_t_a) (g base_t_tb) base_t_cAnd that's it! The function is dense, but the good thing is that the complexity is isolated to a small piece of code. Now that we have defined this distributive law, we could start using it together with gcata and 3 functions as follows:
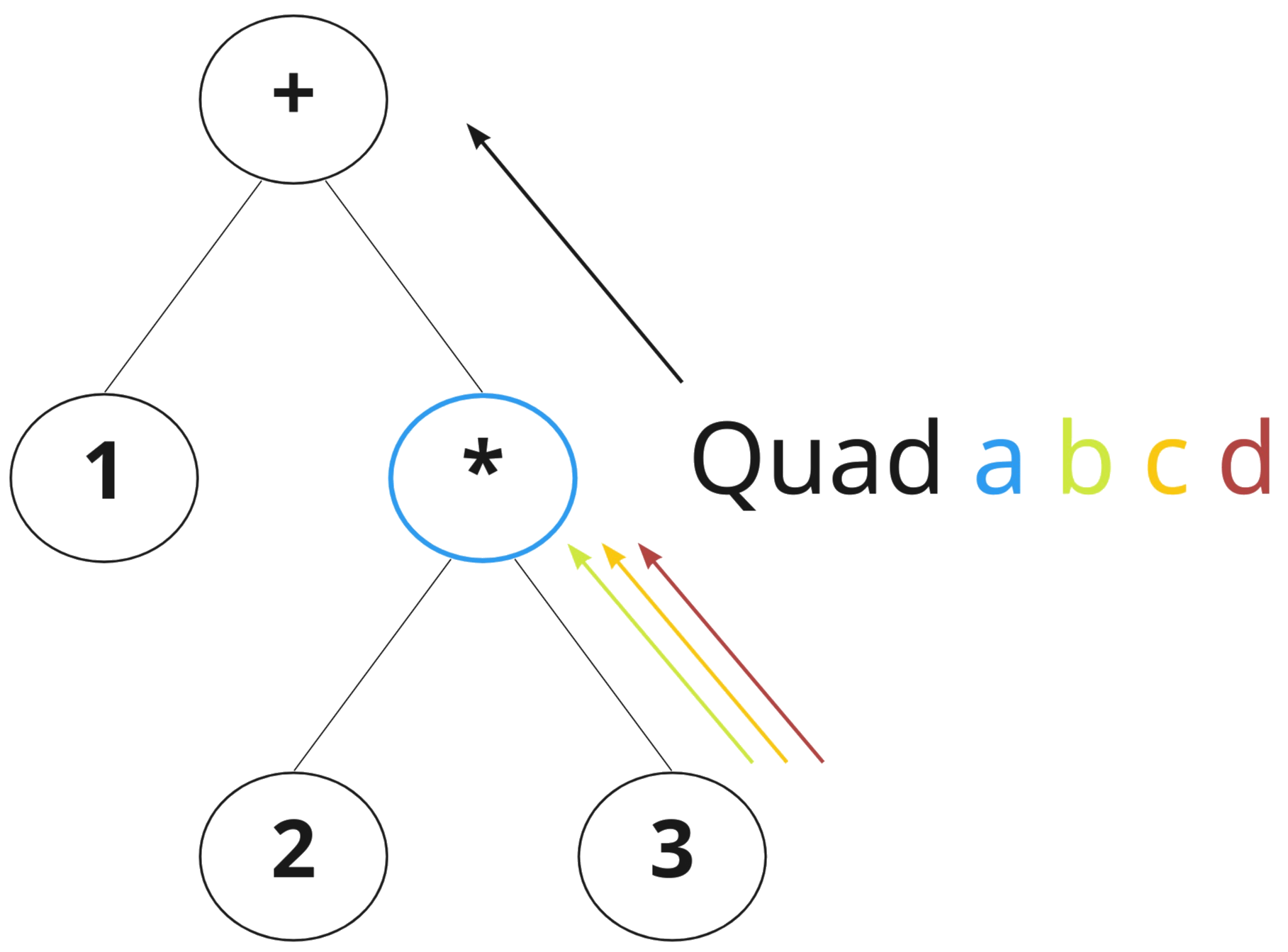
If we try to visualize what's going on, we end up with something like the figure below. During a recursive bottom-up traversal, 3 functions are used to compute the results from the subtrees. These 3 results are combined with the node itself and stored in the Quad datatype, and passed onto the next level up in the tree.

As a final note, you can extend this technique to an N-ary tuple, allowing you to do N+1 simultaneous folds over a recursive structure. On top of that, the performance will still only be O(n) (with n equal to the size of the recursive structure), since the results from the subtrees are computed and collected on the fly while traversing the recursive structure. And since Haskell is lazy, if you don't use those sub-results, they won't even get evaluated!
Conclusion
In this post I showed how comonads in combination with the extremely general gcata function can be used to create tailor-made recursion schemes. By providing our own Comonad type and following a mechanical process for defining a distributive law, we can create a recursion scheme that does exactly what we need.
If you want to see a couple of places where I use this technique in action, you can look here for the actual code using Quad and here for a similar example using Triple for LLVM code generation. The technique proved to be very valuable, since the specialized recursion-scheme helped me structure the different moving parts of a complex pass in my Datalog compiler. Be warned though that both examples are not that straight-forward since they are quite large.
Finally, if you have any questions or thoughts about this article, let me know on Twitter.