Analyses are arrows
In today's post, I explore how we can use Haskell to compose multiple Soufflé Datalog analyses in an elegant and principled way using various Haskell type-classes. No deep knowledge of Soufflé Datalog or the souffle-haskell library is expected, but I do expect some familiarity with the more often used type-classes (Functor, Applicative, ...).
The Analysis data type
As a quick recap, the souffle-haskell library provides bindings for interacting with Soufflé Datalog. All functionality is provided via a SouffleM monad, which focuses on a single Datalog analysis / program. Like I mentioned in my blogpost about "Static analysis using Haskell and Datalog", an analysis consists of a few distinct parts:
- Find all relevant facts related to our Datalog analyses (in Haskell),
- Explicitly "run" Soufflé to compute all derived facts,
- Collect all results back on the Haskell side.
We can make this idea first-class by turning this into a Haskell datatype, giving us the following:
-- NOTE: "Handle prog" is a type-safe handle of a Datalog program
data Analysis prog input output
= Analysis (Handle prog -> input -> SouffleM ()) -- finding facts
(Handle prog -> SouffleM ()) -- running Soufflé
(Handle prog -> SouffleM output) -- retrieving resultsNow that we have this new type, let's try writing some instances for it. First of, let's start with the Functor instance. This will make it possible to transform the result of an analysis:
instance Functor (Analysis prog input) where
fmap f (Analysis find run get) =
Analysis find run (fmap (fmap f) get)Besides Functor, we can also implement Profunctor. This gives us the ability to transform the input type of an analysis (using lmap):
instance Profunctor (Analysis prog) where
lmap f (Analysis find run get) =
Analysis (\h -> lmap f (find h)) run get
rmap = fmapSemigroup and Monoid instances are also possible, but they don't provide much additional value on top of what souffle-haskell already provides with the SouffleM monad. I chose to provide them anyway, because maybe somebody else has a good usecase for it (and the instances are straight-forward anyway) 😉.
instance Semigroup output => Semigroup (Analysis prog input output) where
Analysis find1 run1 get1 <> Analysis find2 run2 get2 =
Analysis (find1 <> find2) (run1 <> run2) (get1 <> get2)
instance Monoid output => Monoid (Analysis prog input output) where
mempty = Analysis mempty mempty memptyNext up is Applicative. Implementing this for our Analysis type enables us to combine two different analyses from multiple Datalog programs with the same input type using applicative-style programming. We can try creating an instance for this type-class, but we would hit a snag when we try to use it. To find out why, take a look at the (<*>)-operator, specialized for our analysis type:
It may not be immediately obvious, but the prog type-variable has to be the same for both arguments passed to the operator! If you recall, this type-variable is used by the Handle type to keep track of the Datalog program it belongs to. Because the type-variable needs to stay the same for both arguments, we can't compose 2 different Datalog programs like this. We also can't get rid of this phantom type-variable, because this is what makes it possible for souffle-haskell to perform many compile-time checks as I explained in my post about supercharging handles with phantom types.
Luckily, we can circumvent this issue using a trick functional programmers often use: partial application. The trick is to close over the handle, so it no longer appears in our Analysis type, effectively hiding the type-variable. We can do this as follows:
-- No more 'prog' type variable!
data Analysis input output
= Analysis (input -> SouffleM ())
(SouffleM ())
(SouffleM output)
-- An example that shows how to close over a handle in an Analysis:
example :: Handle prog -> Analysis [Edge] [Reachable]
example h =
Analysis (Souffle.addFacts h)
(Souffle.run h)
(Souffle.getFacts h)With this change we need to reimplement our previously defined instances though. By applying hole driven development, we quickly find the following implementations:
instance Functor (Analysis input) where
fmap f (Analysis find run get) =
Analysis find run (fmap f get)
instance Profunctor Analysis where
lmap f (Analysis find run get) =
Analysis (lmap f find) run get
rmap = fmap
-- NOTE: omitting Semigroup and Monoid, these have exactly
-- the same implementations as before.Now we can also implement Applicative without the composition issue mentioned earlier:
instance Applicative (Analysis input) where
pure a = Analysis mempty mempty (pure a)
Analysis find1 run1 get1 <*> Analysis find2 run2 get2 =
Analysis (find1 <> find2) (run1 <> run2) (get1 <*> get2)As a quick side note, the behavior of this instance is very similar to what I described in my post about combining folds with semigroups. For example, with a library like recursion-schemes, a single fold can be performed to find all facts for multiple analyses.
Additional forms of composition
We already achieved quite a bit so far with these first instances, but can we go further? One example that comes to mind is sequential composition. If we can think of a function where the output of one analysis forms the input of another, then it should be possible to execute them one after the other:
After some searching, this is the (flipped) (.)-operator (from Control.Category). However, if we try to implement Category for our analysis type, we run into an issue yet again. This time the issue is with the id :: Analysis a a "constant": for the third argument of the constructor, we can't construct a value of type a out of thin air!
All hope is not lost though. Just like before, we can do a small adjustment to our type (at the cost of rewriting the earlier defined instances all over again):
data Analysis input output
= Analysis (input -> SouffleM ())
(SouffleM ())
(input -> SouffleM output) -- input now also passed in here
-- Helper function, results in same behavior as before.
mkAnalysis :: (input -> SouffleM ())
-> SouffleM ()
-> SouffleM output
-> Analysis input output
mkAnalysis find run get = Analysis find run (const get)
-- The following instances are a good exercise for
-- honing your hole driven development skills:
instance Functor (Analysis input) where
fmap f (Analysis find run get) =
Analysis find run (fmap (fmap f) get)
instance Profunctor Analysis where
lmap f (Analysis find run get) =
Analysis (lmap f find) run (lmap f get)
rmap = fmap
instance Semigroup output => Semigroup (Analysis input output) where
Analysis find1 run1 get1 <> Analysis find2 run2 get2 =
Analysis (find1 <> find2) (run1 <> run2) (get1 <> get2)
instance Monoid output => Monoid (Analysis input output) where
mempty = Analysis mempty mempty mempty
instance Applicative (Analysis input) where
pure a = Analysis mempty mempty (const $ pure a)
Analysis find1 run1 get1 <*> Analysis find2 run2 get2 =
Analysis (find1 <> find2)
(run1 <> run2)
(\input -> get1 input <*> get2 input)With this change, we can now implement Category:
-- NOTE: this function proves it is an isomorphism with `Kleisli SouffleM`
execAnalysis :: Analysis input output
-> (input -> SouffleM output)
execAnalysis (Analysis find run get) input = do
find input
run
get input
instance Category Analysis where
id = Analysis mempty mempty pure
-- remember: right-to-left composition!
Analysis find2 run2 get2 . Analysis find1 run1 get1 =
Analysis find run2 get
where
find = execAnalysis (Analysis find1 run1 get1) >=> find2
get = get1 >=> get2The (.)-operator is a little tricky to implement: we first have to make sure the first analysis has fully executed (all 3 parts), and only then can we start the second analysis. The fetching of results now also requires calling both get1 and get2, but since we are using const in the mkAnalysis helper function, a second additional fetching of results (from get1) is skipped thanks to Haskell's built-in laziness.
This new definition of the Analysis type also makes it possible to implement Arrow and ArrowChoice:
instance Arrow Analysis where
arr f = Analysis mempty mempty (pure . f)
first (Analysis find run get) =
Analysis (find . fst) run $ \(b, d) -> (,d) <$> get b
instance ArrowChoice Analysis where
left (Analysis find run get) = Analysis find' run get'
where
find' = \case
Left b -> find b
Right d -> pure ()
get' = \case
Left b -> Left <$> get b
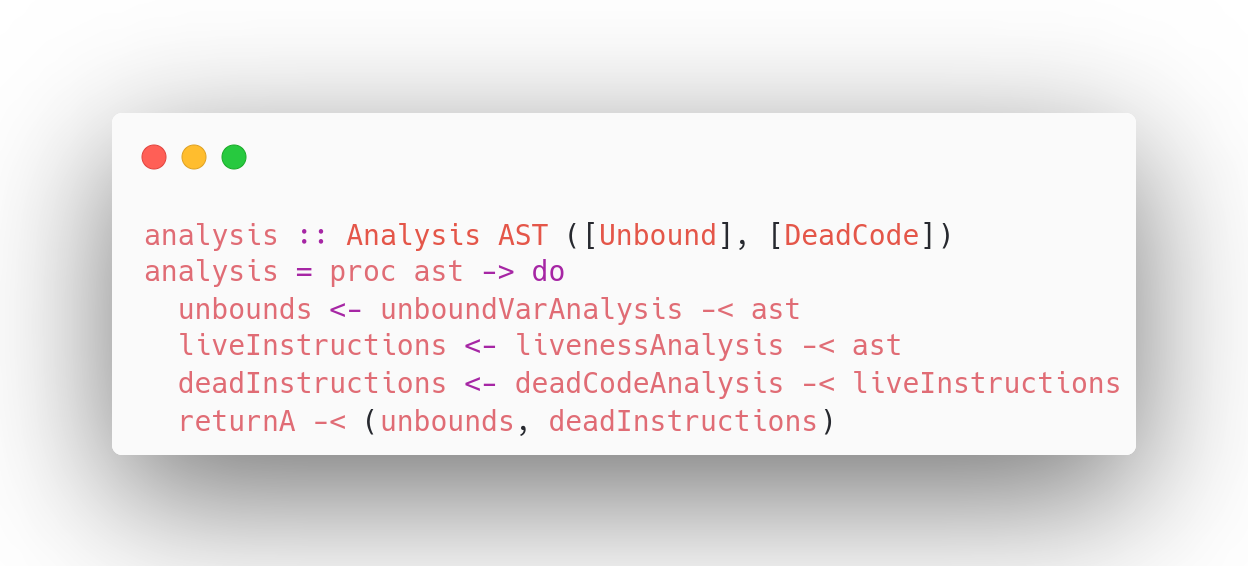
Right d -> Right <$> pure dFinally, armed with all these instances, it now becomes possible to write complex analyses in a data-flow style using arrow notation:
-- Hypothetical example, where both an unbound variable analysis is done,
-- together with a liveness analysis, followed by a dead code analysis.
data AST = ...
data UnboundVar = ...
data Liveness = ...
data DeadCode = ...
unboundVarAnalysis :: Analysis AST [UnboundVar]
livenessAnalysis :: Analysis AST [Liveness]
deadCodeAnalysis :: Analysis [Liveness] [DeadCode]
analysis :: Analysis AST ([UnboundVar], [DeadCode])
analysis = proc ast -> do
unbounds <- unboundVarAnalysis -< ast
liveInstructions <- livenessAnalysis -< ast
deadInstructions <- deadCodeAnalysis -< liveInstructions
returnA -< (unbounds, deadInstructions)Conclusion
In this post I explained my thought process implementing a new analysis type for the souffle-haskell library. By creating a new data type encapsulating the concept of an analysis and by implementing some key type-class instances, it integrates well with the rest of the Haskell ecosystem. This Analysis type will become available in souffle-haskell v2.3.0 (or you can already start experimenting with it by checking out the latest commit).
If you are interested in more content like this, follow me on Twitter. Feel free to contact me if you have any questions or comments about this topic.